Bosonic Pauli+: A tool for designing a quantum computer built from GKP qubits
The Bosonic Pauli+ method can make accurate predictions about large error corrected quantum computers built from superconducting GKP qubits, and will enable us to quickly progress and develop the details of our quantum computer.
At Nord Quantique, we believe that the best way to build a useful quantum computer is using superconducting GKP qubits. Our previous blog posts explain why we believe that, and we have recently achieved an important milestone to get there [1, 2, 3].
Our industry-leading approach is at the cutting edge of research and technology. This means that our scientists and engineers often face technical questions that nobody knows the answer to. For example, in what precise way should many individual GKP qubits be connected to make a useful quantum computer? What is the best way to spread quantum information across several GKP qubits, in order to achieve optimal robustness to errors and noise? How many GKP qubits and how much time are we going to need exactly to perform a given useful quantum computation? Some tentative answers to these questions are known if one uses ordinary qubits instead of GKP qubits, but GKP qubits are fundamentally different!
To answer questions like these, we need to be able to make predictions: Using a classical computer, we need to do an accurate simulation and predict what would happen for many different possible ways of building a quantum computer from our superconducting GKP qubits. The richer nature of GKP qubits, compared to conventional qubits, makes them a promising building block for fault-tolerant quantum computing. At the same time, it makes them especially challenging to simulate, requiring innovative simulation strategies.
To address these challenges, we have developed the Bosonic Pauli+ method. For the first time, this method enables us to make accurate predictions about the performance of a large-scale error corrected quantum computer built from superconducting GKP qubits. It wasn't previously known that a realistic simulation like this is possible! Bosonic Pauli+ (BP+ for short) is thus a unique and exciting tool in our researchers' toolbox, and will enable us to quickly progress and develop the details of our quantum computer.
Background: Simulating Quantum Systems
To understand what BP+ can do and how it is unique, let us start with some background: How do researchers usually simulate quantum systems?
The brute force way: Solving the Schrödinger Equation
Fundamentally, we know that the quantum state of a quantum system can be described by a state vector
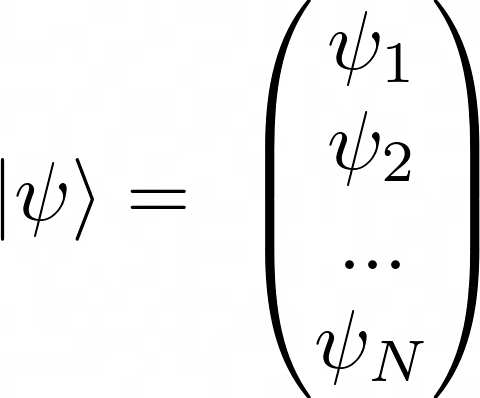
Each of the amplitudes ![]() is a complex number.
is a complex number.
We also know that the way the quantum state changes in time is described by the Schrödinger equation
![]()
The Schrödinger equation, and its cousin called the Lindblad master equation, accurately describe the processes going on inside any kind of quantum computer, including a quantum computer built from GKP qubits. For small quantum systems, the equations can be solved using a classical computer, allowing us to predict what is going to happen.
Unfortunately, there is a catch: for large quantum systems, it quickly becomes impossible for even the best classical computers to handle solving the equations. The issue is that for a system built from not one, but a large number N of physical qubits, the amount of classical memory required to store the quantum state grows exponentially in N. This is already bad for conventional qubits where the required memory is 2ᴺ, but for GKP qubits, 50ᴺ or even 100ᴺ is required.
So it is impossible to simulate a quantum computer with more than a few GKP qubits using this brute force approach.
Clearly, we are going to need other ideas!
|
A Shortcut: Clifford Simulations
We believe that for useful quantum computation, quantum error correction is required [1]. The usual approach to this, different from our approach, is to use many physical qubits to redundantly encode one logical qubit, using what is known as a Quantum Error Correcting (QEC) Code. Usually, each of the physical qubits has exactly two distinct states.
For the common types of QEC codes, the quantum states and quantum operations that occur in an implementation are only a small subset of all possible quantum states and operations. This can be exploited to bypass the brute-force approach: we don't have to save all the amplitudes of the state. Using what's known as Clifford simulations, even large QEC codes built from conventional two-level qubits can be simulated efficiently on a classical computer.
The realization that efficient simulations of standard QEC codes are possible has been quite important in the history of fault tolerant quantum computing, unlocking discoveries which would otherwise have been impossible to obtain. All the more reason to find ways of efficiently simulating our non-standard GKP systems!
Unfortunately, Clifford simulations only work for conventional two-level qubits, not for GKP qubits. So our problem is still unsolved.
|
Bosonic Pauli+
Let's take stock: by solving the Schrödinger or the Lindblad master equation, we can accurately simulate a few GKP qubits. Using the Clifford approach, we can simulate QEC codes with many non-GKP qubits. Can we have the best of both worlds?
Let us envision a quantum computer which uses a QEC code designed for conventional two-level qubits, but replace some of the ordinary qubits with GKP qubits. This approach is a promising way to build a GKP quantum computer. In this situation, we have two layers of QEC codes: the "inner" code is a GKP code, and the "outer" code is a conventional QEC code. Can we simulate that?
As we saw, the brute-force approach is not practical for such large simulations. Another simple way would be to pretend the GKP qubits are conventional qubits and use Clifford simulations. However, this would throw away everything that is special about GKP qubits, and lead to inaccurate predictions.
It turns out we can have the best of both worlds! Our approach, which we call Bosonic Pauli+, has two steps:
Firstly, we developed a simplified yet accurate description of our implementation of a GKP qubit: In the simulation, the GKP qubit is described as a conventional two-level qubit, plus a small amount of additional information. This additional information contains a record of the physical errors and noise processes which have affected the GKP qubit. Obtaining this description required developing a new theoretical way of distinguishing between logical quantum information and information about various kinds of errors for an individual GKP qubit. This way takes into account the specific structure of our GKP implementation. Secondly, adopting ideas from a method called Pauli+ [4], we extended the framework of Clifford simulations to be able to process the additional error information.
One of the things that make building a quantum computer from GKP qubits so promising is that while performing the error correction of each GKP qubit, some information can be gathered. This information can then be used to significantly boost the performance of the outer code, potentially allowing to reach low error rates with a low qubit count. The BP+ method takes these intricate interactions between the two layers of error correction into account.
A limitation of the BP+ method is that currently, it does not work for every way in which GKP qubits can be combined to build an error-corrected quantum computer: While many promising approaches can be simulated with BP+, others will require further development of the method. We're on it, stay tuned!
|
Impact
Using the Bosonic Pauli+ model, we were able to predict the performance of a logical qubit obtained by using many GKP qubits as building blocks in a conventional QEC code. This was not previously possible, with existing approaches being too inefficient, or not accurate enough for simulating our GKP implementation.
Having BP+ in our toolbox has opened up many exciting avenues for us. To mention just some: We can now compare the performance of different conventional QEC codes in conjunction with GKP qubits, enabling us to optimize our approach and identify the best route forward. The BP+ method also allows us to pinpoint which physical error mechanisms most affect the performance of logical qubits, thereby identifying which areas to focus on in the development of our hardware and GKP code implementation. Having a way to theoretically separate logical quantum information from information about errors, which is an important component of BP+, is also independently useful.
Last but not least, we hope that the BP+ method will be useful for other companies and academic groups working on bosonic quantum computing, and will help materialize error-corrected quantum computing!
Where can I learn more?
We have posted a research paper on the BP+ method at [5].
We will also present these results at the 2024 March Meeting of the American Physical Society.
[1] What are bosonic codes and why do we love them?
[2] Nord Quantique demonstrates quantum error correction, first company to make a logical qubit out of a physical qubit
[3] Lachance-Quirion, Dany, Marc-Antoine Lemonde, Jean Olivier Simoneau, Lucas St-Jean, Pascal Lemieux, Sara Turcotte, Wyatt Wright, et al. "Autonomous Quantum Error Correction of Gottesman-Kitaev-Preskill States". arXiv, 19 October 2023. https://doi.org/10.48550/arXiv.2310.11400.
[4] Supplementary Information IV in: Google Quantum AI, Rajeev Acharya, Igor Aleiner, Richard Allen, Trond I. Andersen, Markus Ansmann, Frank Arute, et al. "Suppressing Quantum Errors by Scaling a Surface Code Logical Qubit". Nature 614, no. 7949 (23 February 2023): 676–81. https://doi.org/10.1038/s41586-022-05434-1.
[5] Hopfmueller, Florian, Maxime Tremblay, Philippe St-Jean, Baptiste Royer, and Marc-Antoine Lemonde. "Bosonic Pauli+: Efficient Simulation of Concatenated Gottesman-Kitaev-Preskill Codes". arXiv, 14 February 2024. https://doi.org/10.48550/arXiv.2402.09333.