Early Fault Tolerance with Bosonic Codes

At Nord Quantique, we implement resource-efficient Quantum Error Correction (QEC) using bosonic codes in superconducting architectures. This approach enables direct error correction on key physical components through advanced control protocols, eliminating the need for hardware redundancy. This method offers a clear path towards a one-to-one logical qubit to physical cavity ratio, to achieve fault tolerant quantum computing (FTQC) without the burden of excessive hardware overhead.

Our team recently released a preprint sharing our vision for building utility-scale quantum computers. As the quantum computing industry continues to mature, there is widespread acknowledgement that useful quantum computation will require fault tolerance. Machines capable of FTQC will have the ability to correct errors and enable longer and more complex computations to be performed. Progress on error correction will pave the way for new applications, relevant for industrial users of quantum computing. 

At Nord Quantique we’ve identified three critical areas which can drive the field forward toward FTQC with QEC at scale:

• Hardware efficiency: The ability to correct errors without requiring massive hardware overheads will lead the industry to meaningful quantum error-correction, sooner. For example, some platforms might require up to 1,000 physical qubits to encode a single error corrected qubit. Slashing that overhead by orders of magnitude is essential to propel quantum computing into the fault tolerant era. 
• Scalability: Quantum computing platforms containing anywhere from 100 to 1,000 physical qubits are becoming more common. However, with those ratios, achieving fault tolerance without hardware-efficient error correction could require computers with over a million qubits. Building such large systems is an extraordinary challenge, one which is further complicated by the need to address problems with scaling control electronics and cryogenic infrastructure. At Nord Quantique, we believe scalability should refer to the ability to reach utility-scale (and beyond) by using a more realistic amount of these resources.  This belief is entwined with the notion of hardware efficiency, and minimizing requirements at all levels of the quantum computing stack.
• Fast Clock Speeds: The total time it takes to run a quantum algorithm is important. Even with exponential speedups in terms of number of logical operations compared to classical computing, the ability to perform such logical operations fast is crucial in providing an advantage for users. 

In our preprint, entitled Hardware-Efficient Fault Tolerant Quantum Computing with Bosonic Grid States in Superconducting Circuits, we outline what our team perceives as the most viable path to FTQC, and how we intend to get there. This includes uniquely designed hardware, bosonic codes, and fast clock speeds built into superconducting systems. 

Quantum Error Correction and Efficient Fault Tolerance

The number of qubits in quantum computers has long been a key measure of industry progress. While it remains a useful indicator of engineering advances, this metric alone overlooks the fact that unlocking a broader range of practical applications will require significant improvements in the performance of the qubits themselves. Enhancements in hardware and control alone are unlikely to achieve the performance needed for quantum computing to reach its full potential.

A key component to overcoming this challenge is the implementation of QEC, which will be essential for ensuring computational accuracy at scale. Therefore, we believe that resource-efficient hardware architectures such ours, which minimize the qubit overhead required for error correction, will be key to unlocking most practical quantum applications.

For example, Nord Quantique’s first bosonic qubit achieved a 1.2X performance improvement using this QEC method, implemented on a single superconducting cavity. In contrast, recent advancements on other superconducting platforms have demonstrated similar gains, around 2X, but have required up to 100 physical qubits to achieve those results. Thus, making them far less efficient than the solution we propose. QEC demonstrations using bosonic codes have also been conducted by academic groups, where over the past decade, the field has witnessed consistent advancements without requiring additional physical overhead. This progress underscores their potential as a practical solution for achieving the performance levels necessary for real-world applications. 

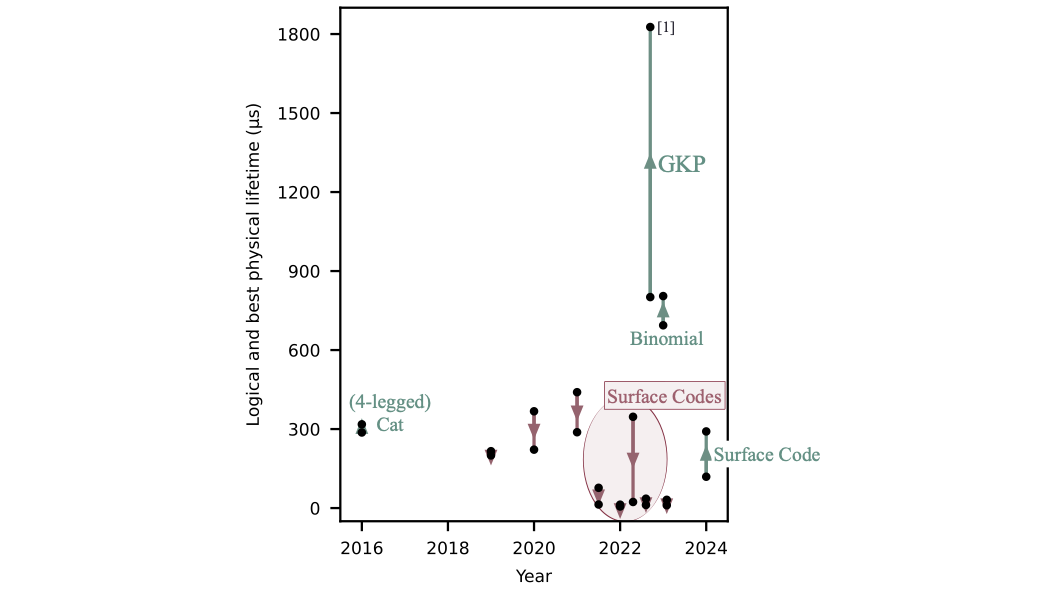
Figure 1: Review of the QEC attempts to go beyond the break-even point in superconducting circuits, beyond which the performance of an error-corrected logical qubit exceeds that of its best physical constituent; that is the point at which performing QEC overall improves the qubit logical coherence. The logical lifetime of the logical qubit after QEC is compared to the logical lifetime of the best physical constituent in the system. Green upward arrows (red downward) represent demonstrations beyond (below) the break-even point.

How does it work?

Error correction is not unique to quantum computing - it is widely used in many critical technologies to eliminate errors in signals. For instance, error correction protocols are integral to communication technologies like 5G. Both classical and quantum error correction rely on encoding redundant information to prevent local errors from corrupting the original message, typically requiring additional bits (or qubits) for encoding and processing. For quantum computing, this is where bosonic codes change the game by naturally offering logical redundancy within a single physical element.

While various bosonic codes can be utilized, such as cat qubits and binomial codes, the team at Nord Quantique has chosen to focus on grid codes. With the appropriate control protocols, grid codes can autonomously correct both bit and phase flips, paving the way for the implementation of a full set of fault-tolerant operations necessary for utility-scale quantum computing on a resource-efficient platform. Expanding beyond the single-mode encoding used in all previous demonstrations (i.e. GKP qubits), multimode grid states - where the code resides in a multimode cavity - allowing for more sophisticated code constructions that can either mitigate or improve the detection of additional error types, such as those arising from control errors. This multimode approach introduces minimal overhead compared to single-mode codes, especially when leveraging multimode cavities, providing a significant advantage for scalability by maintaining a one-to-one ratio of logical qubits to physical cavities.

In the paper, we describe how to efficiently encode, correct, manipulate, and decode logical information in bosonic grid states using superconducting circuits. The following superconducting elements enable the full control of a bosonic grid code.

1. High coherence 3D multimode cavity
2. Nonlinear auxiliary element (e.g. the transmon)
3. Readout resonator 

These components provide an essential toolbox for autonomous QEC and fast single-qubit operations. The architecture for FTQC is built on tiling superconducting cavities, each equipped with its auxiliary elements and readout, and hosting error-corrected grid states. For two-qubit gates, active couplers link the cavities, enabling the controlled activation and deactivation of interactions between neighboring cavities.

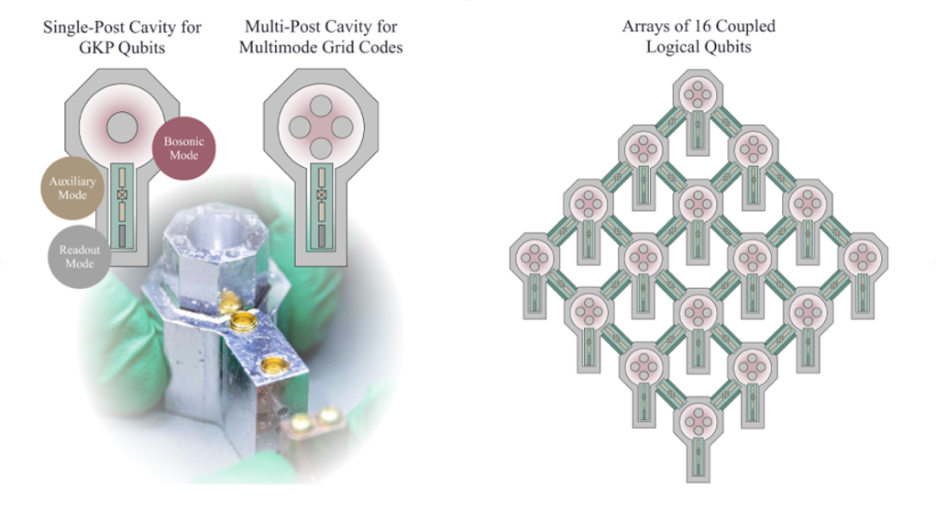
Figure 2: Hardware architecture for error-corrected quantum processors based on bosonic multimode grid states in 3D superconducting circuits.

Going beyond utility-scale: How confidence information can help 

Existing research suggests that grid states alone have the potential to achieve the performance required for utility-scale FTQC. However, to reach vanishing logical error rates and go beyond utility scale, grid states can be concatenated with more conventional binary error-correction codes, such as quantum Low-Density Parity-Check (qLDPC) codes. Specifically, this involves implementing qLDPC codes in which each qubit is an error-corrected grid state, enhancing the overall error correction and performance.

In this context, a key advantage of grid states is that, during autonomous QEC protocols, they provide valuable real-time information about the reliability of each individual qubit. This confidence data can be used to enhance the decoding process in qLDPC qubit codes, leading to further performance improvements.

The same architecture offers a new computational paradigm

Finally, the architecture proposed by the team at Nord Quantique for implementing resource-efficient QEC to achieve early FTQC can also support a novel computational paradigm. This paradigm combines quantum continuous variables (CV), such as bosonic modes in cavities, with discrete variables (DV), represented by the auxiliary modes, to create a hybrid CV-DV computational model. Recent research has systematically developed the CV-DV quantum instruction set for this architecture and proposed quantum algorithms optimized for such a setup. This computational model is particularly well-suited for quantum simulations, where both electronic and vibronic structures are crucial for understanding material properties.

Conclusion

Bosonic encodings offer a promising solution to the scaling challenges faced by more traditional QEC strategies, which typically rely on hardware redundancy by increasing the number of individually controlled physical two-level systems. In contrast, multimode grid states in superconducting circuits have the potential to achieve FTQC with a one-to-one ratio between superconducting cavities and logical qubits, capable of operating with fast clock speeds in the MHz range. This hardware efficiency also significantly reduces the infrastructure requirements to support a utility-scale quantum computer, creating an efficient pathway towards early, fully scalable fault-tolerant quantum computing using superconducting circuits.