What are bosonic codes and why do we love them?
The fundamental components that allow a quantum computer to carry out computations are its qubits. A qubit can store quantum information in any of the two logical states, 0 and 1, like a classical bit, but also in some superposition of these two states — that's what makes them quantum! Logical states are abstract, though. They are "made real" through what we call an encoding (or code), which can be as simple as choosing two distinct physical states of a given quantum device (e.g. a physical qubit) to represent the logical states 0 and 1 used in computations.
In most QC platforms, the physical qubit is designed in such a way that it has precisely two distinct states that are easily addressed and manipulated for computations. With a superconducting qubit for instance, those two states are typically chosen as the ground state |g〉 and the first excited state |e〉 of the physical qubit. In this case the encoding is direct and there is no important distinction between what we call the "logical" qubit (used to perform computations) and the "physical" qubit (the actual physical component) since one can always simply associate these states one-to-one
![]()
If the equations above look trivial, it's because they are! But then, why would anyone use other non-trivial encodings? In what follows, we will show a few examples of more complex encodings that inherently improve the robustness of a qubit against common quantum computer issues.
All that noise!
Any quantum experimentalist will tell you: quantum computers are unfortunately quite sensitive to undesired interactions with the outside world — a phenomenon called noise. For instance, physical qubits in an excited state tend to suddenly switch to their ground state — we call this qubit relaxation.
If we were simply using the direct encoding as above, then it's easy to see that the logical state has also switched, most likely introducing errors into the computation.
For this reason, we tend to refrain from using the words "logical qubits" when talking about those two-level physical qubits, since they can't really be used to perform logical operations due to those errors.
The good news is that there are ways to deal with those errors, a process known as quantum error correction. In most systems, error correction can only be implemented by using additional physical resources in order to provide redundancy of information (in the form of extra physical qubits). For instance, one could encode a logical qubit using three physical qubits instead of just one, in the following way:
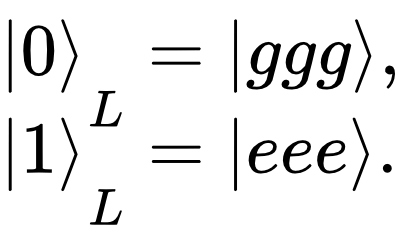
Note that the distinction between logical and physical qubit is more clear in this case: the state of a single logical qubit is now distributed over three separate physical components. It also means that some states of the whole system no longer represent valid logical states. For instance, assuming that one starts with the 1 logical state — encoded physically as |eee⟩ — and that the second physical qubit accidentally relaxes to its ground state, we'd end up in the state
![]() .
.
which does not correspond to a valid logical state. This actually is not a significant issue as we could in principle detect the presence of this error, and correct it in place using a majority vote (2 out of 3 are in the e state, so we'd assume we started in |eee⟩).
![]()
However, the procedure above would fail if the system suffered from errors happening on two physical qubits at about the same time. This is why the overhead for error correction via physical redundancy is much higher than the three-for-one ratio in our example. Rather, this overhead is expected to be on the order of thousands to tens of thousands of physical qubits per logical qubit in most architectures, and even these large ratios are considered too optimistic by some.
Fortunately, there is an alternative to this costly overhead. By using physical components that can address more than just two states, the necessary redundancy can be obtained almost "for free" at this level. This is what is referred to as a bosonic code, and this is the technology we are developing at Nord Quantique.
The beauty of bosonic codes
It's possible to build quantum physical components allowing for more than two individually addressable states. Examples include trapped ion systems, and microwave photons inside superconducting cavities, which is the technology we develop here at Nord Quantique.
With our technology, these addressable states are simply the number of individual photons contained in a cavity — as well as any superposition of these states. In principle there is no limit to the number of photons one could stuff inside a single cavity. In practice though, it is easier — and sufficient — to use encodings that involve only a few photons (say using less than a hundred or so).
We still refer to these components as physical qubits, which is a bit of a misnomer considering that they are much more interesting than their two-level counterparts. Their added capabilities are made clear by the fact that it is possible to implement an error-corrected logical qubit in a single physical qubit under this system. This is what we set out to do at Nord Quantique.
To be fair, since error correction in the real world is bound to be imperfect, we would still expect to benefit from some level of physical redundancy on top of that. But it's a reasonable goal to have this overhead reduced by orders of magnitude when compared to standard two-level physical qubits, and we believe this is what we'll need in order to build a useful, fault-tolerant quantum computer at scale.
A working example: the binomial code
How then can we exploit this inherent redundancy in order to implement error-corrected logical qubits? Let's illustrate with an example code, whereas the logical qubit would be defined in the following manner:
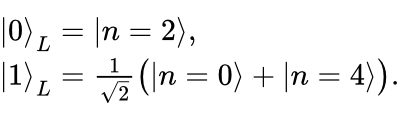
The variable n here represents the state associated to n photons being in the cavity.
Now what happens if the system suffers from the loss of a photon? The logical states would be affected in the following way:
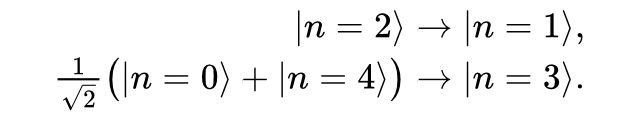
This is analogous to what we saw when using physical redundancy of qubits: the system ends up in a state that no longer represents a logical state, but both states are still distinguishable and can in principle be corrected.
This is an example of a bosonic code: implementing a logical qubit in a single component, with the ability to perform (at least some) error correction at this level. This particular example is called a binomial encoding.
One issue with this specific example is that we haven't yet solved the problem of two errors occurring at the same time — or perhaps of a second error occurring before we had time to correct the first.
To solve this issue, we need other bosonic codes that can provide additional protection
when more errors occur. Here are two of the best-known examples of this.
Cat code
A cat code is an example of a bosonic code that provides additional protection against certain types of errors. To describe this code and its logical states, we must introduce a new type of state available in bosonic qubits known as coherent states. A coherent state consists of a specific superposition of all possible photon number states. There is an infinite family of such states, each labeled by an arbitrary complex number. For the cat encoding, we can use some real positive number β to define the 0 logical state, and the value -β for the logical 1:
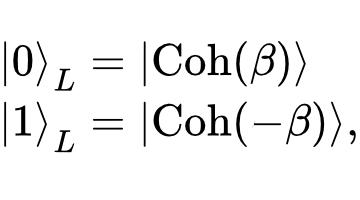
One of the great advantages of cat codes is that they rely on a property of the coherent states: under photon loss, coherent states are preserved, up to a pre-factor given by the number that labels it.
Hence under photon loss the cat code logical states become
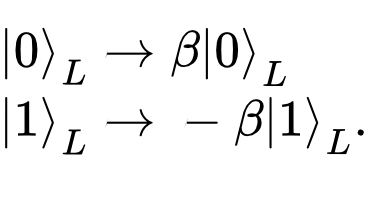
We see that individually, each of the logical states are unaffected by the noise-induced photon loss — the extra pre-factor does not affect the state itself. However, when considering a specific superposition of the two logical states 0 and 1, then those factors become important. Consider the case of the state given by the sum of 0 and 1, and how it transforms after photon loss:
![]()
The logical state has truly changed now, and this change would lead to a computational error.
In error correction parlance, we identify two types of possible quantum errors: bit-flips (whereas a 0 becomes a 1 and vice-versa), and phase-flips, as in the expression above. We would say then that bit-flip errors are suppressed by the cat code (which is great!), but not phase-flips (less great).
One could argue that only the "classical" part of the quantum information is protected by the cat encoding, since we are only guaranteed that the logical 0 remains a 0, and a logical one remains a one. While this is correct, it is important to keep in mind that the logical cat state is still quantum in nature and as such can still be used to perform quantum computations. The limited error correction capability of the cat code only means that there is an unavoidable need for error correction via physical redundancy. The good news is that the requirements for correction of just the phase-flip errors should be much less than those using simple two-level physical qubits.
Everything everywhere all at once: the GKP code
The GKP code1 is a type of bosonic code that can provide protection against both types of error, although it does so at a cost. Under single photon loss, both logical states (and any superposition thereof) are almost perfectly preserved, and the probability of a successful error correction is very high. Yet, if the physical bosonic qubit accumulates many losses before it is corrected, the logical states progressively deteriorate and the probability of a successful correction diminishes accordingly. But if the rate of error correction is high enough to avoid accumulation of errors, then in principle at least the correction could be made as good as it needs to be.
There are different ways to represent the logical states of a GKP code, one of them is through a discrete sum of an infinite number of coherent states, and in that view the GKP code could be seen as a generalization of the cat code. The complex numbers that label the coherent states involved in the GKP logical states form a regular lattice or grid in the complex plane, and as such GKP states are often referred to as grid states. See Fig. 1.

Figure 1. Wigner representation of a GKP logical grid state.
Under photon loss, a logical GKP state will be affected through local deformations of the individual blobs (or peaks), and in particular will widen a bit. Obviously this widening, if not corrected in time, would end up with individual peaks interfering with one another, and eventually losing the information held by the qubit.
What we have not mentioned so far is that there are other ways by which errors can occur in a given device. Interestingly, the approach described above can also be effective in correcting most of these other types of errors.
This is the core of the work being done here at Nord Quantique. Our efforts have been paying off. Recently we have shown that we can indeed correct errors on logical GKP states, and most importantly that we can do it at a faster rate than they occur, opening up the path towards fault-tolerant quantum computing at scale.
The details of how we managed to achieve this quantum error correction milestone will be the subject of our next blog post. Stay tuned!
1D. Gottesman, A. Kitaev, and J. Preskill, Physical Review A 64, 012310 (2001).