Technical Paper: Suppressing Logical Errors with Multimode Quantum Error Correction
Nord Quantique - May 28, 2025
I. INTRODUCTION
Quantum error correction (QEC) is essential for fault-tolerant quantum computing, ensuring that logical information remains protected from physical noise during the execution of quantum algorithms. Traditional QEC strategies achieve this by redundantly encoding logical qubits across many physical two-level systems (qubits), but this approach incurs significant hardware overhead, making large-scale fault-tolerant quantum computing (FTQC) a daunting challenge. While recent small-code demonstrations have made progress, they either operate above threshold, lack scalability, or do not incorporate mid-circuit measurements [1–5].
An alternative paradigm is bosonic codes, which leverage the large Hilbert space of quantum oscillators to perform error correction within a single physical mode, offering a potentially more hardware-efficient path to FTQC [6]. Grid codes are a class of bosonic codes that encode discrete-variable logical information in translationally invariant lattices in phase space [7]. They are particularly promising for quantum error correction, as studies suggest that single-mode grid codes effectively correct photon loss errors and outperform other single-mode bosonic codes [8, 9]. Experimental demonstrations have validated its error correction capabilities [10–13]. Notably, error correction above breakeven—where the encoded logical lifetime surpasses the bare oscillator lifetime—has been achieved [11, 13], and autonomous quantum error correction has also been demonstrated for single-mode grid codes [12].
A key challenge with grid code-encoded qubits is designing the system such that photon loss remains the dominant error channel. In practice, experimental implementations face additional complications, particularly due to auxiliary control systems (e.g., transmons), which can introduce other sources of errors. Single-mode grid state encoding is particularly vulnerable to such auxiliary errors, as errors occurring during the stabilizer protocol often directly generate logical errors. This can lead to silent logical errors that remain undetected and uncorrected, limiting the effectiveness of single-mode grid codes.
To make fault-tolerant quantum computing (FTQC) with grid codes viable, three strategies have been proposed:
- Concatenating grid qubits with outer error-correcting codes [14–17]
- Using noise-biased or error-transparent auxiliaries [18]
- Employing multimode grid codes [6, 7, 19–22]
The last approach leverages multiple bosonic modes to encode logical qubits, increasing robustness against auxiliary-induced errors. With multimode grid encodings, it is possible to devise codes in which auxiliary errors during stabilization move the state outside the logical space rather than inducing silent logical errors. This allows error syndromes to be detected via measurements, making error correction more effective.
A notable example is the Tesseract code, a two-mode grid code that introduces emergent features beyond single-mode implementations. One of its key advantages is the isthmus property, which reduces the impact of auxiliary decay errors [20]. Unlike standard singlemode grid code implementations, where auxiliary decay can lead to undetected logical errors, the Tesseract code ensures that such errors leave detectable signatures, allowing them to be identified and mitigated through post-processing. This makes multimode grid codes a promising pathway toward fault-tolerant quantum computing [6].
In this work, we present the first experimental realization of a multimode grid code, demonstrating its enhanced features by leveraging mid-circuit measurement outcomes to suppress logical decay in a hardware-efficient architecture [6].
II. MULTIMODE TOOLBOX: HARDWARE AND ENTANGLING GATE
Building on theoretical proposals, we realized a full in-house demonstration of multimode grid code state preparation and quantum error correction, bridging concept to implementation within a scalable hardware platform.
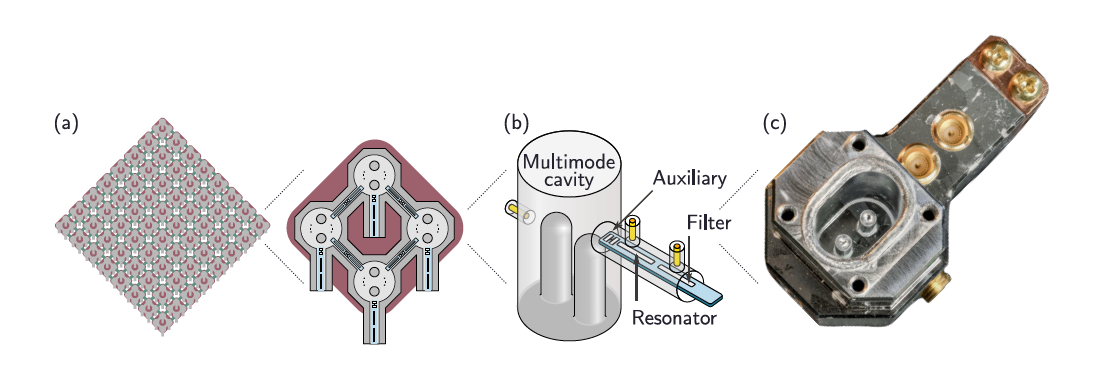
FIG. 1. (a) Schematic of the FTQC architecture of Ref. [6] based on interconnected multimode units, in which each multimode unit is an encoded logical qubit. (b) Schematic of the singleunit multimode hardware platform. A single auxiliary transmon is dispersively coupled to the two normal oscillator modes of the double-post cavity, as well as a on-chip readout and filter resonators. (c) Photo of a two-mode prototype.
A. Multimode Hardware Platform
The Tesseract code was implemented in a single-unit prototype, designed as a foundational building block for a logical qubit in a scalable multimode architecture, as outlined in Ref. [6] and briefly sketched in Fig. 1(a). This prototype demonstrates how a single unit can encode and process logical information while remaining compatible with a larger, extensible quantum computing platform.
Each unit consists of a superconducting multimode 3D cavity, where two oscillator modes are controlled by a single auxiliary transmon qubit [Fig. 1(b,c)]. The encoded multimode grid code resides within these two oscillator modes inside the cavity, leveraging their large Hilbert space for quantum information storage and error correction. This platform enables universal control over multiple bosonic modes without additional hardware overhead, making it a scalable approach to multimode quantum error correction [6]. A readout resonator coupled to the auxiliary qubit allows for logical measurements across both modes.
B. Multimode Echoed Conditional Displacement Gate
The Echoed Conditional Displacement (ECD) gate is a fundamental tool for controlling grid code qubits [10, 23]. Originally developed for single-mode systems, this gate extends naturally to multimode architectures [Fig. 2], enabling entangling operations between bosonic modes without additional complexity.
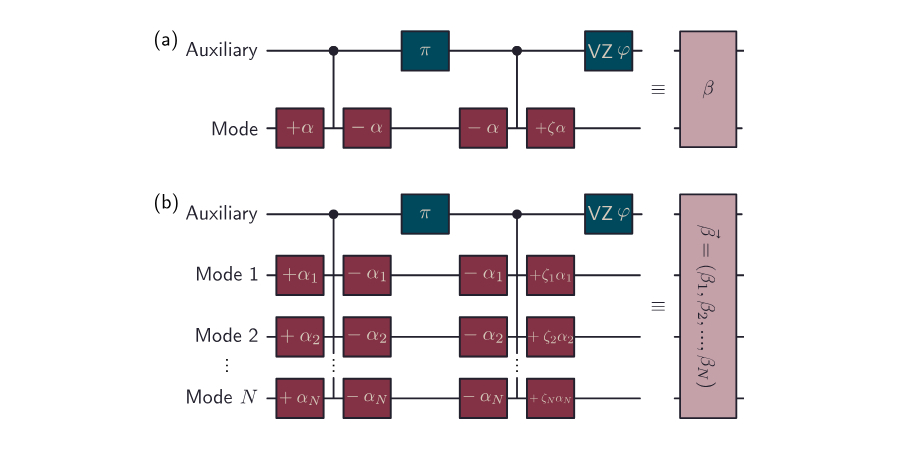
FIG. 2. (a) Single-mode echoed conditional displacement β composed of displacements ±α, auxiliary echo π pulse, free evolution under a static dispersive interaction, and an auxiliary virtual Z gate of phase φ. The last displacement pulse is scaled by a factor ζ to correct for displacement errors. (b) Extension to multimode echoed conditional displacements ⃗β = (β1, β2, . . . , βN), in which the size of the displacements αn are used to achieve a conditional displacements of amplitude βn.
The multimode ECD entangling gate offers several key advantages:
- Limited additional calibration required compared to the single-mode implementation.
- Same fidelity and duration as single-mode ECD gates for equivalent amplitudes.
- No χ-matching required, significantly simplifying implementation.
This efficient multimode entangling operation plays a crucial role in enabling logical operations for multimode bosonic error correction, making it a powerful tool for scalable quantum computing.
III. MULTIMODE GRID CODE: STATE PREPARATION AND ERROR CORRECTION
A. State Preparation
The Tesseract code extends single-mode grid encoding by distributing logical information across two bosonic modes. Logical states |± ¯ Z⟩ correspond to two unentangled single-mode rectangular grid states, one in each mode. In contrast, logical states | ± ¯X ⟩ and | ± ¯ Y ⟩ are prepared by entangling these single-mode grid states. More generally, a sequence of auxiliary rotations and two-mode ECD gates is sufficient to prepare any logical state [Fig. 3(a)].
Figure 3(e-v) presents experimentally measured two-dimensional slices of the six logical states of the Tesseract code. These slices intersect all Pauli and stabilizer operators of the code [Fig. 3(b-d)], providing a complete characterization of the logical states. The prepared logical states achieve a fidelity of FL = 0.86 for Δ = 0.45, corresponding to an average of two photons per mode.
B. Autonomous Quantum Error Correction
Now that we have demonstrated, for the first time, the successful state preparation of the Tesseract code, we turn to the next crucial step: implementing quantum error correction to protect the encoded logical information.
We implemented a fully autonomous QEC protocol for the Tesseract logical qubit, illustrated in Fig. 4(a). This corresponds to the two-mode generalization of the sBs protocol [20, 24], incorporating a fully autonomous auxiliary reset as demonstrated in Ref. [12]. Mid-circuit measurements are integrated into the protocol, and their impact on QEC performance is examined in the next section.
The performance of autonomous QEC for the multimode grid code is evaluated in the restless regime, where the idle time is set to zero to minimize errors per QEC cycle. In this configuration, each QEC round has a duration of 2.77 μs. The logical fidelity is analyzed as a function of the number of QEC rounds, as shown in Fig. 4(b). In this regime, we measure the logical error per round to be εsBs = 2.1(1) × 10−2.
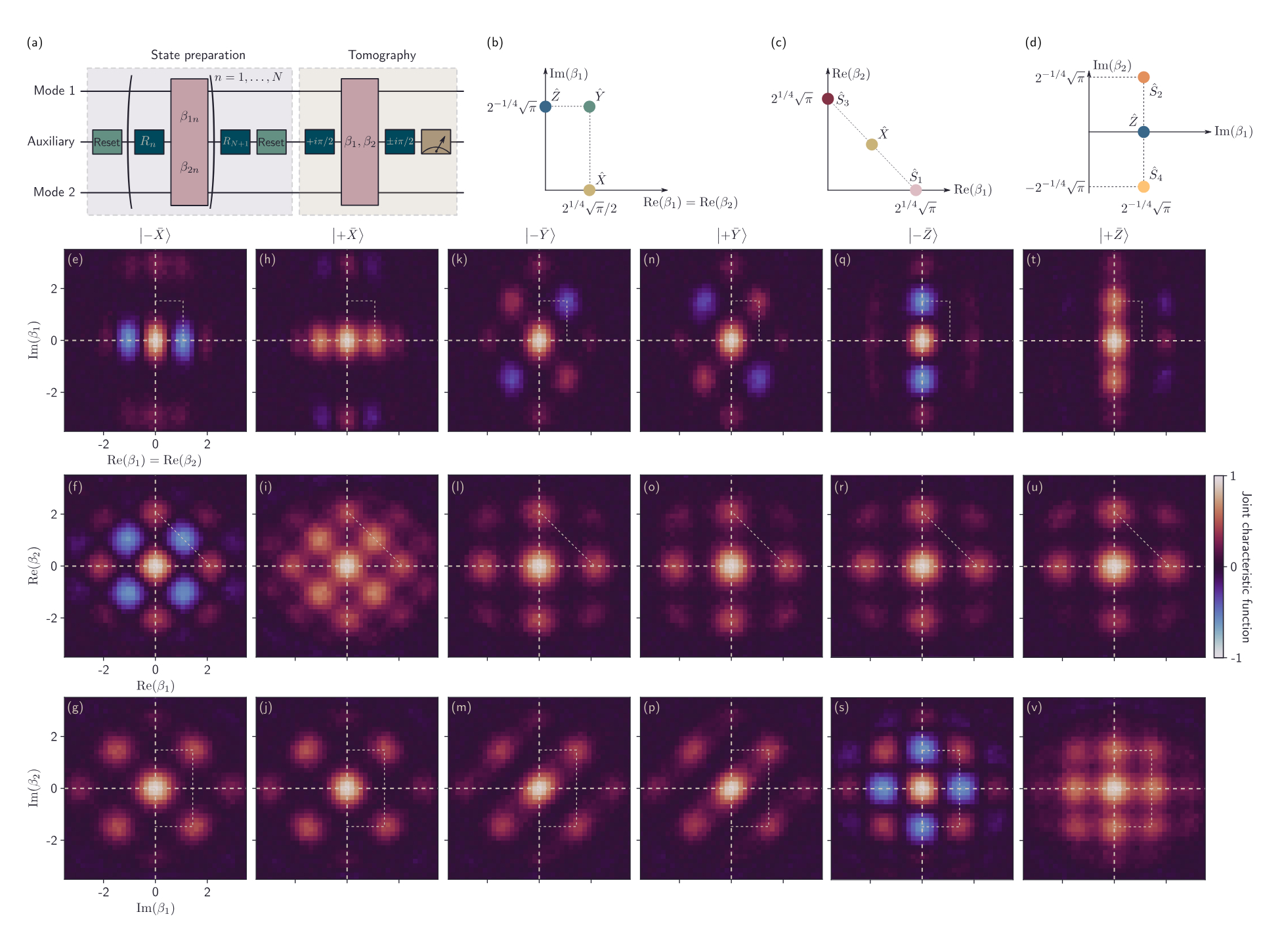
FIG. 3. (a) State preparation protocol for the Tesseract grid code. Two-dimensional planes that includes (b) all Pauli operators ˆX , ˆ Y , and ˆ Z, (c) single-mode stabilizer operators ˆ S1 and ˆ S3, and (d) two-mode stabilizers ˆ S2 and ˆ S4. (e-v) Experimental 2D slices of the real part of the joint characteristic function C(β1, β2) for the six logical Pauli states (e-j) | ± ¯X ⟩, (k-p) | ± ¯ Y ⟩, and (q-v) | ± ¯ Z ⟩ of the Tesseract qubit with finite-energy parameter Δ = 0.45.
C. Mid-Circuit Measurements
Mid-circuit measurements are a standard feature of quantum error correction, allowing error syndromes to be extracted and processed by a decoder to correct logical errors in real time. In our implementation, mid-circuit measurements are integrated into the autonomous sBs QEC protocol [Fig. 4(a)] to extract confidence information about the multimode grid code logical qubit. Importantly, the protocol remains fully autonomous, as the auxiliary qubit is reset after each measurement, ensuring continuous operation without active feedback.
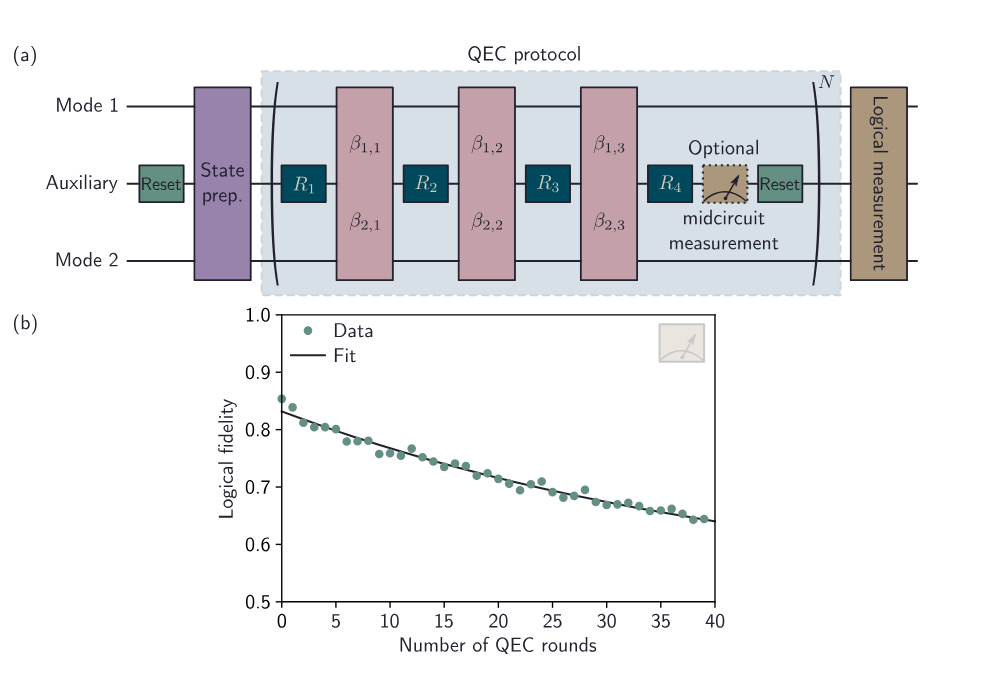
FIG. 5. (a) Example of mid-circuit measurement outcomes for 16 QEC rounds with green (yellow) indicated the auxiliary ground (excited) state. In the full erasure limit, a valid shot, indicated in blue, is one where all measurements outcomes correspond to the auxiliary ground state. (b) Survival probability as a function of the number of QEC rounds. The line indicates an exponential decay from which the rejection probability prej = 12.6(2)% is obtained. (c) Increase of logical error as a function of the number of QEC rounds without erasure (burgundy) and with full erasure (teal). The full line corresponds to the exponential fit from which the logical error per round εsBs = 3.5(3)×10−2 is obtained. The horizontal dashed line indicate the absence of an increase of the logical error.
As shown in Fig. 5(c), when mid-circuit measurement outcomes are not used, the logical error per round is measured to be εsBs = 3.5(3) × 10−2. This is comparable to the logical error rate observed in the protocol without mid-circuit measurements [Fig. 4(b)], taking into account the increased duration of each QEC cycle from 2.77 μs to 3.73 μs. These results indicate that the inclusion of mid-circuit measurements does not significantly degrade QEC performance.
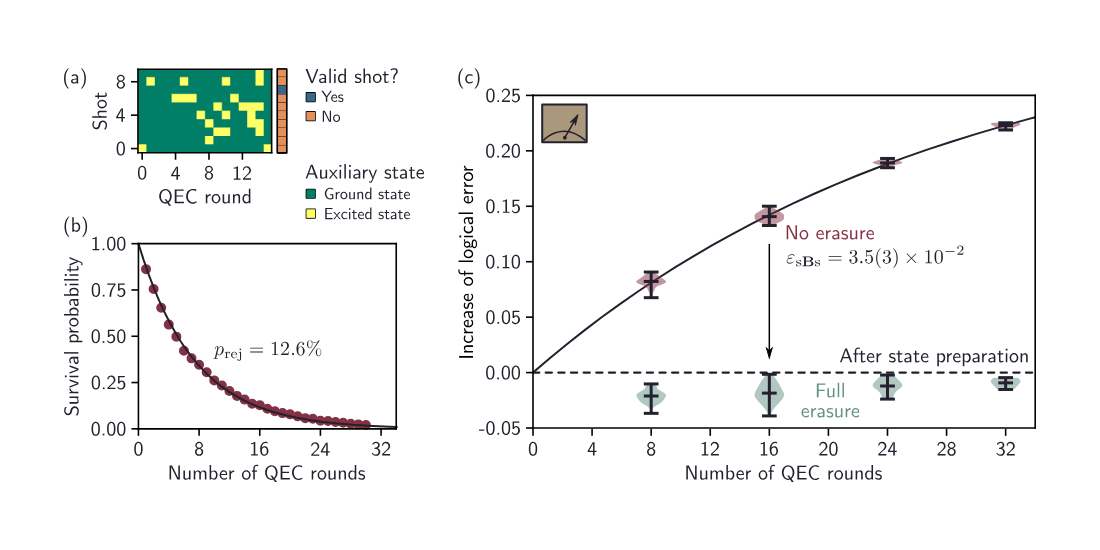
FIG. 5. (a) Complete protocol used to prepare, correct, and measure Tesseract logical states. The QEC protocol, corresponding to the two-mode sBs protocol, is composed of auxiliary rotations Rn and twomode conditional displacements of amplitudes (β1,n, β2,n). An optional mid-circuit measurement can be performed before the autonomous auxiliary reset. Logical measurements are performed with either an infinite- or finite-energy protocol [24]. (b) Logical fidelity as a function of the number of QEC rounds in the absence of mid-circuit measurements, indicating a logical error per round εsBs = 2.1(1) × 10−2.
D. Leveraging Confidence Information for Erasure-Based Error Suppression
Beyond monitoring the logical qubit through end-of-the-line measurements only, the confidence information extracted from mid-circuit measurements can be actively used to improve error correction. By identifying and discarding potentially flagged realizations, we can achieve stronger logical protection—an approach known as erasure-based error suppression.
As illustrated in Fig. 5(a), in the full erasure limit, measurement shots with at least one flagged error are discarded, leading to a rejection probability of 12.6% [Fig. 5(b)]. This relatively high rejection probability increases the experimental cost of extending beyond the 32 QEC rounds explored here. In this regime, the survival probability of a given experimental realization is only about 1.3%, making longer experiments increasingly impractical. The fidelity of the mid-circuit measurements used in this implementation, approximately 95%, suggests room for improvement in future iterations.
Unlike single-mode grid codes, where displacements of half a lattice spacing remain undetected, the Tesseract code identifies these errors with high probability [6], enabling significantly improved error suppression. In the full erasure limit, we achieve no observable logical decay over 32 QEC rounds, underscoring the effectiveness of this approach [Fig. 5(c)]. While intermediate erasure strategies could help reduce the rejection probability, their development remains a subject for ongoing work. These results stand in stark contrast to those of single-mode grid codes. In Ref. [11], applying the full erasure limit reduced the logical error per round by only a factor of 6.3. In contrast, in our implementation, no statistically resolvable loss of logical information is observed after 32 QEC rounds.
IV. CONCLUSION
Our experimental realization of the Tesseract code demonstrates how multimode bosonic codes introduce emergent features that go beyond single-mode implementations. In addition to increasing the number of logical qubits, multimode grid codes provide a complementary scaling axis by increasing the number of modes per logical qubit. This expanded encoding strategy enhances error correction capabilities and opens new avenues for fault-tolerant quantum computing. These features include:
- The isthmus property, which reduces the impact of auxiliary decay errors.
- The suppression of silent errors, leading to enhanced logical lifetimes.
- The ability to extract confidence information, improving error detection and correction strategies.
Unlike previous grid-state implementations, the Tesseract code ensures that a single auxiliary decay cannot cause undetected logical errors, significantly enhancing fault tolerance. These advancements mark an important milestone toward scalable, hardware-efficient quantum error correction. This work aligns with Nord Quantique’s roadmap toward achieving scalable fault-tolerant quantum computing using hardware-efficient bosonic codes.
Want to read more?
Download a copy of the full Tesseract Technical Paper.
[1] D. Bluvstein, S. J. Evered, A. A. Geim, S. H. Li, H. Zhou, T. Manovitz, S. Ebadi, M. Cain, M. Kalinowski, D. Hangleiter, J. P. B. Ataides, N. Maskara, I. Cong, X. Gao, P. S. Rodriguez, T. Karolyshyn, G. Semeghini, M. J. Gullans, M. Greiner, V. Vuleti´c, and M. D. Lukin, Logical quantum processor based on reconfigurable atom arrays, Nature 626, 58 (2024).
[2] C. Ryan-Anderson, N. C. Brown, C. H. Baldwin, J. M. Dreiling, C. Foltz, J. P. Gaebler, T. M. Gatterman, N. Hewitt, C. Holliman, C. V. Horst, J. Johansen, D. Lucchetti, T. Mengle, M. Matheny, Y. Matsuoka, K. Mayer, M. Mills, S. A. Moses, J. Pino, P. Siegfried, R. P. Stutz, J. Walker, and D. Hayes, High-fidelity teleportation of a logical qubit using transversal gates and lattice surgery, Science 385, 1327 (2024).
[3] B. W. Reichardt, D. Aasen, R. Chao, A. Chernoguzov, W. van Dam, J. P. Gaebler, D. Gresh, D. Lucchetti, M. Mills, S. A. Moses, B. Neyenhuis, A. Paetznick, A. Paz, P. E. Siegfried, M. P. da Silva, K. M. Svore, Z. Wang, and M. Zanner, Demonstration of quantum computation and error correction with a tesseract code, arXiv:2409.04628 (2024).
[4] M. J. Bedalov, M. Blakely, P. D. Buttler, C. Carnahan, F. T. Chong, W. C. Chung, D. C. Cole, P. Goiporia, P. Gokhale, B. Heim, G. T. Hickman, E. B. Jones, R. A. Jones, P. Khalate, J.-S. Kim, K. W. Kuper, M. T. Lichtman, S. Lee, D. Mason, N. A. Neff-Mallon, T. W. Noel, V. Omole, A. G. Radnaev, R. Rines, M. Saffman, E. Shabtai, M. H. Teo, B. Thotakura, T. Tomesh, and A. K. Tucker, Fault-tolerant operation and materials science with neutral atom logical qubits, arXiv:2412.07670 (2024).
[5] P. S. Rodriguez, J. M. Robinson, P. N. Jepsen, Z. He, C. Duckering, C. Zhao, K.-H. Wu, J. Campo, K. Bagnall, M. Kwon, T. Karolyshyn, P. Weinberg, M. Cain, S. J. Evered, A. A. Geim, M. Kalinowski, S. H. Li, T. Manovitz, J. Amato-Grill, J. I. Basham, L. Bernstein, B. Braverman, A. Bylinskii, A. Choukri, R. DeAngelo, F. Fang, C. Fieweger, P. Frederick, D. Haines, M. Hamdan, J. Hammett, N. Hsu, M.-G. Hu, F. Huber, N. Jia, D. Kedar, M. Kornjaˇca, F. Liu, J. Long, J. Lopatin, P. L. S. Lopes, X.-Z. Luo, T. Macr`ı, O. Markovi´c, L. A. Mart´ınez-Mart´ınez, X. Meng, S. Ostermann, E. Ostroumov, D. Paquette, Z. Qiang, V. Shofman, A. Singh, M. Singh, N. Sinha, H. Thoreen, N. Wan, Y. Wang, D. Waxman-Lenz, T. Wong, J. Wurtz, A. Zhdanov, L. Zheng, M. Greiner, A. Keesling, N. Gemelke, V. Vuleti´c, T. Kitagawa, S.-T. Wang, D. Bluvstein, M. D. Lukin, A. Lukin, H. Zhou, and S. H. Cant´u, Experimental demonstration of logical magic state distillation, arXiv:2412.15165 (2024).
[6] M.-A. Lemonde, D. Lachance-Quirion, G. Duclos-Cianci, N. E. Frattini, F. Hopfmueller, C. Gauvin-Ndiaye, J. Camirand-Lemyre, and P. St-Jean, Hardware-efficient fault tolerant quantum computing with bosonic grid states in superconducting circuits, arXiv:2409.05813 (2024).
[7] D. Gottesman, A. Kitaev, and J. Preskill, Encoding a qubit in an oscillator, Physical Review A 64, 012310 (2001).
[8] V. V. Albert, K. Noh, K. Duivenvoorden, D. J. Young, R. T. Brierley, P. Reinhold, C. Vuillot, L. Li, C. Shen, S. M. Girvin, B. M. Terhal, and L. Jiang, Performance and structure of single-mode bosonic codes, Physical Review A 97, 032346 (2018).
[9] G. Zheng, W. He, G. Lee, and L. Jiang, The near-optimal performance of quantum error correction codes, arXiv:2401.02022 (2024).
[10] P. Campagne-Ibarcq, A. Eickbusch, S. Touzard, E. Zalys-Geller, N. E. Frattini, V. V. Sivak, P. Reinhold, S. Puri, S. Shankar, R. J. Schoelkopf, L. Frunzio, M. Mirrahimi, and M. H. Devoret, Quantum error correction of a qubit encoded in grid states of an oscillator, Nature 584, 368–372 (2020).
[11] V. V. Sivak, A. Eickbusch, B. Royer, S. Singh, I. Tsioutsios, S. Ganjam, A. Miano, B. L. Brock, A. Z. Ding, L. Frunzio, S. M. Girvin, R. J. Schoelkopf, and M. H. Devoret, Real-time quantum error correction beyond break-even, Nature 616, 50–55 (2023).
[12] D. Lachance-Quirion, M.-A. Lemonde, J. O. Simoneau, L. St-Jean, P. Lemieux, S. Turcotte, W. Wright, A. Lacroix, J. Fr´echette-Viens, R. Shillito, F. Hopfmueller, M. Tremblay, N. E. Frattini, J. Camirand Lemyre, and P. St-Jean, Autonomous quantum error correction of gottesman-kitaev-preskill states, Physical Review Letters 132, 150607 (2024).
[13] B. L. Brock, S. Singh, A. Eickbusch, V. V. Sivak, A. Z. Ding, L. Frunzio, S. M. Girvin, and M. H. Devoret, Quantum error correction of qudits beyond break-even, Nature 641, 612 (2025).
[14] K. Noh and C. Chamberland, Fault-tolerant bosonic quantum error correction with the surface–gottesman-kitaev-preskill code, Physical Review A 101, 012316 (2020).
[15] K. Noh, C. Chamberland, and F. G. Brand˜ao, Low-overhead fault-tolerant quantum error correction with the surface-gkp code, PRX Quantum 3, 010315 (2022).
[16] N. Raveendran, N. Rengaswamy, F. Rozpedek, A. Raina, L. Jiang, and B. Vasi´c, Finite rate qldpc-gkp coding scheme that surpasses the css hamming bound, Quantum 6, 767 (2022).
[17] F. Hopfmueller, M. Tremblay, P. St-Jean, B. Royer, and M.-A. Lemonde, Bosonic pauli+: Efficient simulation of concatenated gottesman-kitaev-preskill codes, Quantum 8, 1539 (2024).
[18] A. L. Grimsmo and S. Puri, Quantum error correction with the gottesman-kitaev-preskill code, PRX Quantum 2, 020101 (2021).
[19] J. Harrington and J. Preskill, Achievable rates for the gaussian quantum channel, Physical Review A 64, 062301 (2001).
[20] B. Royer, S. Singh, and S. Girvin, Encoding qubits in multimode grid states, PRX Quantum 3, 010335 (2022).
[21] M. Lin, C. Chamberland, and K. Noh, Closest lattice point decoding for multimode gottesmankitaev- preskill codes, PRX Quantum 4, 040334 (2023).
[22] J. Conrad, J. Eisert, and F. Arzani, Gottesman-kitaev-preskill codes: A lattice perspective, Quantum 6, 648 (2022).
[23] A. Eickbusch, V. Sivak, A. Z. Ding, S. S. Elder, S. R. Jha, J. Venkatraman, B. Royer, S. M. Girvin, R. J. Schoelkopf, and M. H. Devoret, Fast universal control of an oscillator with weak dispersive coupling to a qubit, Nature Physics 18, 1464–1469 (2022).
[24] B. Royer, S. Singh, and S. M. Girvin, Stabilization of finite-energy gottesman-kitaev-preskill states, Physical Review Letters 125, 260509 (2020).